昨天講了 SVM 模型在做二元分類的原理、概念,今天來講如何將 SVM 用在分類多種類的類別上以及將 SVM 應用在迴歸問題上的 SVR 。
SVM本身是一種「二元分類器(binary classifier)」,換句話說,一個SVM的模型,只能處理分類一個具有兩種類別(2 classes)的資料。所以在處理多元分類的問題時,就常會用到以下兩種解法/策略:
[補充]在 R e1071套件裡的svm( ),自動使用One-against-One來解決多元分類的問題。
方法是針對每一個類別,分別建立一個SVM(或其他二元分類器),如果有 T 個類別的資料,就會生成出 T 個 SVM。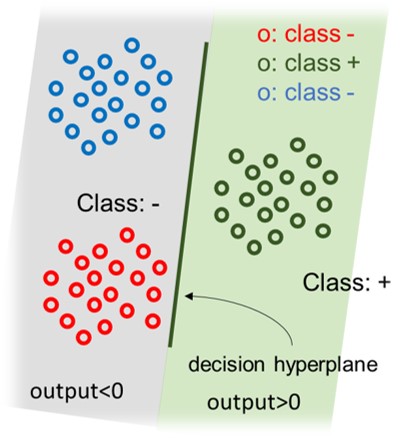
在建立每個類別的 SVM 模型時,屬於此類別的樣本視為(+正),其他類別的樣本視為(-負),如此一來就轉換成一個二元分類的問題了(適用 SVM 二元分類器)。
當有一筆新資料要預測時,會將新資料分別丟進這 T 個 SVM ,此時會輸出 T 組判斷值,再從中找出最大判斷值對應到的類別,那這筆資料便是屬於那一類。其中的 判斷值=(+1/-1)x(資料點到超平面的距離)。因此距離「分類超平面」 越遠越不容易被分錯成那類。
[註- ] OVA 的缺點是在建立各類別的 svm 模型時,將「剩下不是這類別」的資料們視為同一個類別(-負)的這種做法,很容易導致兩類(+/-)之間的資料筆數差距很大,也就會產生資料類別不平衡(class imbalance)的問題。
從多元類別(multi classes)的資料中,任選某兩個類別(2 classes)的資料,訓練一個SVM(只能區分這兩個類別),並重複這樣的動作,直到所有的類別組合,都有其對應的 SVM 為止。也就是說當有 T 種類別時,會生成 C{T取2} = (T(T−1))/2 個 SVM 模型。
當有一筆新資料要預測時,會分別丟進這 (T(T−1))/2 個SVM,每一個SVM都會將這筆資料分到某一類,就像是投票一樣,該類別會記錄+1,最後判斷哪一個類別獲得最多票數,即可預測這筆資料屬於哪一個類別。
[註- ] 要運行計算的時間較長,吃比較多記憶體。分類的類別太多時不適合使用。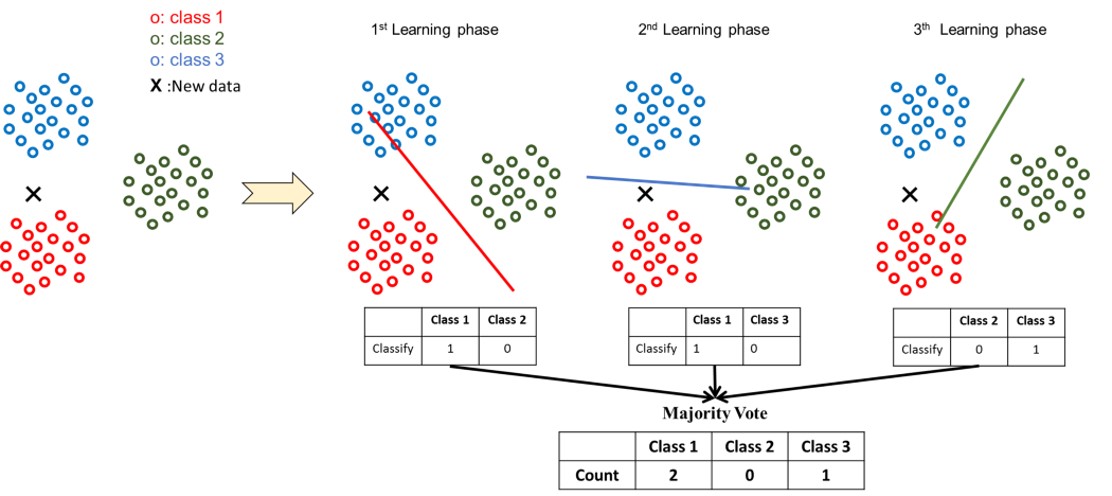
| 方法 | 優點 | 缺點 |
|---|---|---|
| One-against-Rest | 做法很直覺。執行時間與記憶體並不會消耗太多。 | 要注意類別不平衡(class imbalance)的問題。 |
| One-against-One | 不會造成類別不平衡的問題 | 運行時間較長,吃較多的記憶體,不適合太多分類別時使用。 |
SVR (Support Vector Regression)是 SVM 的延伸型態,能夠用來處理連續的預測問題。原理是去找到一個迴歸式,讓所有數據點到迴歸式的距離最近。
在e1071套件裡面,並沒有一個函式叫做 svr( ),而是一樣用svm()。
差別只在於:
依變數的型態是factor時,svm()會建立SVM的超平面,來處理分類問題。
依變數的型態是numeric時,svm()會自動轉為SVR,進行連續值的預測。
所以在 R 裡建立 SVR 模型時記得要檢查資料型態。
SVR vs. Logistic Regression(LR)
這裡使用 R 套件mlbench中的資料「 Glass」來做簡單的示範。
這是一個分類問題,資料中記錄了七種玻璃材質(type)的折光率和不同化學元素含量(8種) 。
共有214個觀測值,10個變數:
輸出變數(Y): 分類別(六種玻璃材質:Type1,2,3,5,6,7);
輸入變數(X): 折光率、化學元素含量(Na, Mg, Al, Si, K, Ca, Ba, Fe)
## Glass dataset 觀察資料型態
install.packages("mlbench")
library(mlbench) # Glass dataset
data("Glass")
head(Glass)
summary(Glass)
str(Glass) # 確定Type的資料形態要是Factor!!
table(Glass$Type)
set.seed(123) # 固定sample()抽樣的結果
train_rows<- sample(x=1:nrow(Glass), size=ceiling(0.80*nrow(Glass) ))
train<- Glass[train_rows,] # 80%當training data
test <- Glass[-train_rows,]# 20%當testing data
使用 R 裡e1071套件svm( )的函式建立基礎的 SVM 模型。
install.packages("e1071")
library(e1071)
model0<-svm(Type ~ .,data=Glass,
type='C', # classification
kernel='radial' ,# Kernel function: radial basis
cost=10)
summary(model0)
在SVM中,一般會去調的參數是(cost, gamma),這邊使用套件內建的tune()的函式調整參數:
# Tune cost and gamma in SVM(soft-margin)
#訓練一堆模型,包含cost=10^-1, 10^0, 10^1, 10^2,gamma=0.1,0.5, 1, 2
tune.model=tune(svm,
Type~.,
data=Glass,
kernel="radial", # RBF kernel function
range=list(cost=10^(-1:2),
gamma=c(0.5,1,2))# 調參數的最主要一行
)
summary(tune.model)
R 裡e1071套件內建tune()的函式,可以幫助我們調整參數,它會自動引入cross validation的手法,確保模型的可靠度(Robustness),讓tune出來的參數是可以採用的。
Parameter tuning of ‘svm’:
- sampling method: 10-fold cross validation
- best parameters:
cost gamma
10 0.5
- best performance: 0.291342
- Detailed performance results:
cost gamma error dispersion
1 0.1 0.5 0.5651515 0.15827513
2 1.0 0.5 0.3326840 0.11734117
3 10.0 0.5 0.2913420 0.13028713
4 100.0 0.5 0.3380952 0.12591707
5 0.1 1.0 0.5463203 0.13849507
6 1.0 1.0 0.3465368 0.12665349
7 10.0 1.0 0.3238095 0.10548331
8 100.0 1.0 0.3378788 0.09974183
9 0.1 2.0 0.5744589 0.13040694
10 1.0 2.0 0.3746753 0.13958177
11 10.0 2.0 0.3614719 0.13591817
12 100.0 2.0 0.3612554 0.12835597
在上面的示範使用 SVM 建模,去預測Glass 資料的分類,訓練的過程中,我們訓練了一堆模型,包含:
cost=10^(−1), 10^0, 10^1, 10^2;
gamma=0.5, 1, 2
這兩種參數的排列組合。換句話說,會有 4x3=12 個SVM模型,然後會從中找出 classification error 最小的組合作為最終模型(這裡報表結果顯示cost=10, gamma=0.5的組合)。
各種組合下的 classification error
plot(tune.model) # classification error
## 如果覺得顏色不明顯,你也可以套上別的色。
library('unikn')
plot(tune.model,color.palette=rainbow) #彩紅色
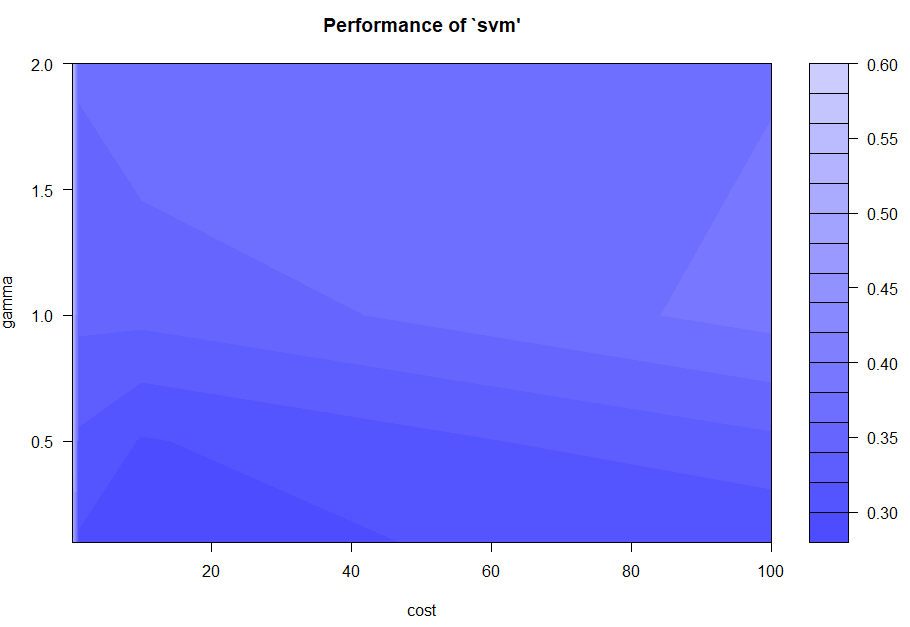
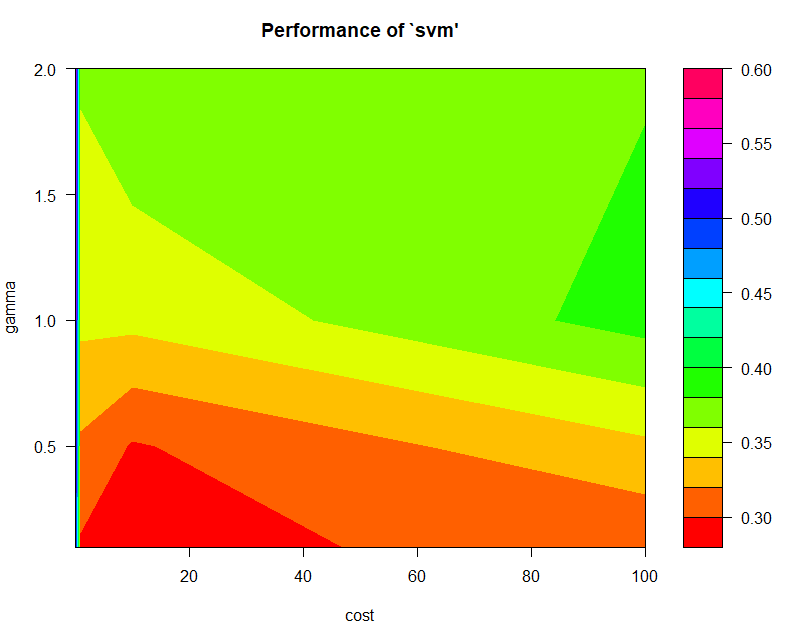
最終模型:
final.model<-svm(Type ~ .,data=Glass,
type='C', # classification
kernel='radial' ,# radial basis
cost=10,
gamma=0.5)
summary(model2)
train.pred = predict(final.model, train)
test.pred = predict(model, test)
# 訓練資料的混淆矩陣
table(predict=train.pred, actual=train$Type)
mean(train.pred==train$Type)# 訓練資料的分類準確率
# 測試資料的混淆矩陣
table(predict=test.pred, actual=test$Type)
mean(test.pred==test$Type)# 測試資料的分類準確率
> # 訓練資料的混淆矩陣
> table(predict=train.pred, actual=train$Type)
actual
predict 1 2 3 5 6 7
1 51 2 0 0 0 0
2 3 58 0 0 0 0
3 1 1 13 0 0 0
5 0 0 0 12 0 0
6 0 0 0 0 7 0
7 0 0 0 0 0 24
> mean(train.pred==train$Type)# 訓練資料的分類準確率
[1] 0.9593023
> # 測試資料的混淆矩陣
> table(predict=test.pred, actual=test$Type)
actual
predict 1 2 3 5 6 7
1 12 2 3 0 1 0
2 3 13 1 0 0 1
3 0 0 0 0 0 0
5 0 0 0 1 0 0
6 0 0 0 0 1 0
7 0 0 0 0 0 4
> mean(test.pred==test$Type)# 測試資料的分類準確率
[1] 0.7380952
這邊示範自己生成資料,並建立 SVR 模型:
test.x<-seq(0.1,5,by=0.05)
test.y<-log(test.x)+rnorm(length(test.x),sd=0.25)
df = data.frame(x=test.x,y=test.y)
head(df)
> head(df)
x y
1 0.10 -2.6019260
2 0.15 -1.6805285
3 0.20 -1.3933998
4 0.25 -1.6859500
5 0.30 -1.0440998
6 0.35 -0.4422655
svr.model<-svm(y~x, data=df, # Y: numeric
type='eps') # eps-regression
summary(svr.model)
svr.pred = predict(svr.model, df)# 預測的點
plot(df$x, df$y, cex=0.5,pch=16, xlab="X", ylab="Y") # 資料的原始值(黑點)
points(df$x,svr.pred,cex=0.5,pch=16, col="blue") # SVR的預測值(藍點)
legend("right",legend=c('data points','svr.pred'),col=c('black','blue'),pch=16)
## 調整參數
tune.model = tune(svm,y~x,data=df,
range=list(cost=c(10,100,500), # 調參數
epsilon = c(0.01,0.1,0.5,1,2)))
#裡面的值是mean squared error
summary(tune.model)
svr.model2<-svm(y~x, data=df, # Y: numeric
type='eps', # eps-regression
cost=10,
epsilon=0.05)
summary(svr.model2)
svr.pred2 = predict(svr.model2, df)# svr model 2預測的點
plot(df$x, df$y, cex=0.5,pch=16, xlab="X", ylab="Y") # 資料的原始值(黑點)
points(df$x,svr.pred,cex=0.5,pch=16, col="blue")
points(df$x,svr.pred2,cex=0.5,pch=16, col="red") # SVR2的預測值(紅點)
legend("right",legend=c('data points','svr.pred','svr.pred2'),col=c('black','blue','red'),pch=16)
[注意] 在 tuning SVR-Parameter時,這裡指的是 mean square error 。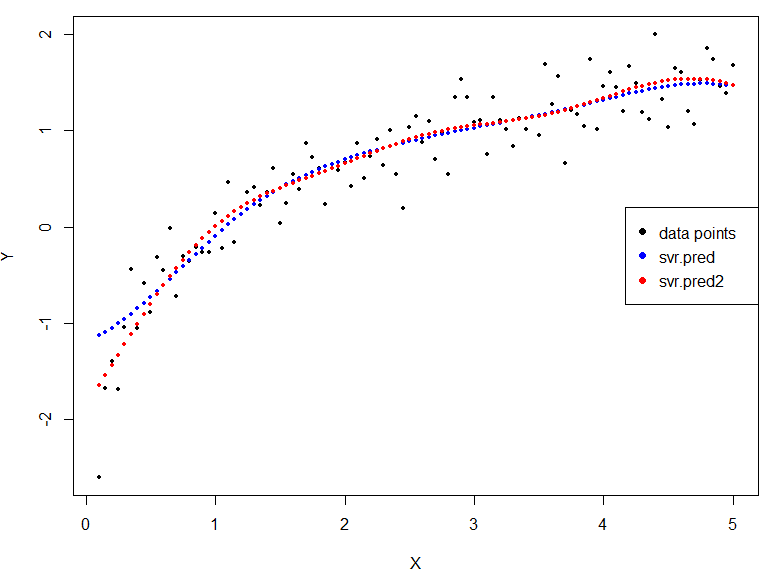
機器學習:如何在多類別分類問題上使用用二元分類器進行分類(Multiclass Strategy for Binary classifier)
https://chih-sheng-huang821.medium.com/%E6%A9%9F%E5%99%A8%E5%AD%B8%E7%BF%92-%E5%A6%82%E4%BD%95%E5%9C%A8%E5%A4%9A%E9%A1%9E%E5%88%A5%E5%88%86%E9%A1%9E%E5%95%8F%E9%A1%8C%E4%B8%8A%E4%BD%BF%E7%94%A8%E7%94%A8%E4%BA%8C%E5%85%83%E5%88%86%E9%A1%9E%E5%99%A8%E9%80%B2%E8%A1%8C%E5%88%86%E9%A1%9E-multiclass-strategy-for-binary-classifier-b4e5017202ff
R筆記 – (14)Support Vector Machine/Regression(支持向量機SVM)
https://rpubs.com/skydome20/R-Note14-SVM-SVR
https://machinelearningmastery.com/one-vs-rest-and-one-vs-one-for-multi-class-classification/
